About 8 or ten years ago I started thinking about doing a graphics demo for the demo scene. I started to prepare a minimum skeleton that should compile to the smallest possible exe. Over the years I kept this Skeleton alive going from Windows XP to Windows 7 and from DirectX 8 to DirectX 10.
More than three years ago I put the source code up on Google Code here and kept updating it:
http://code.google.com/p/graphicsdemoskeleton/
Although the source code is rather short, I played around with many ideas over the years. I read articles by the demo scene about getting smaller exe's just by using Visual Studio. After realizing that my exe got bigger with every new Visual Studio version, I switched to Pelles C; a free development environment with a compiler that follows the C99 standard:
http://www.smorgasbordet.com/pellesc/
My exe is now 838 bytes in size without violating Windows rules about releasing occupied resources. I tried to replace some of the code with assembly code, especially the entry points of the D3D functions and saved a few bytes at some point in time but removed it again because it was too inconvenient.
At some point (probably while it was running on DirectX 9) I implemented a small GPU particle system that didn't add much to the size, which was pretty cool.
One of the interesting things I found out was that HLSL code was packing in some cases smaller than C code for the CPU. I found this remarkable and I thought it would be a cool idea to write a small CPU stub and then go from there in HLSL.
I know there will be times when I go back to this piece of code and wonder what else I can do with it and spend half an hour looking through it. It was certainly the project with some of the lowest priorities in the last ten years ... maybe you can take the source and do something cool with it :-)
There is also a whole demo framework released by Inigo Quelez here
http://www.iquilezles.org/www/material/isystem1k4k/isystem1k4k.htm
Other useful links are:
http://yupferris.blogspot.com/
http://4klang.untergrund.net/
Sunday, September 18, 2011
Wednesday, September 14, 2011
DirectX 11.1 Notes
I plan to update this blog in the next couple of days with more information as soon as it becomes available.
The upgrade from DirectX 11 to DirectX 11.1 is targeting the following areas:
1. Use UAV's at every Pipeline stage
2. Use logical operations in a render target
3. Shader tracing: looks like a new way to measure shader performance
The functions (ID3D11Device::CheckFeatureSupport / ID3D11Device::CheckFormatSupport) that check for supported features and formats were extended as well. D3D11_FEATURE_DATA_ARCHITECTURE_INFO seems to be for tiled-based rendering hardware commonly used in mobile GPUs and D3D11_FEATURE_DATA_SHADER_MIN_PRECISION_SUPPORT too. DXGI_FORMAT was extended to support video formats that now can be processed with shaders by using resource views (SRV/RTV/UAV). There is a new D3D_FEATURE_LEVEL_11_1 defined (i.e. a minor revision of the hardware feature set), but I don’t (yet) have a good link to give you to summarize the required features. Of course, there’s no public drivers or hardware out yet that exposes FL 11.1 anyhow. As before, DirectX 11.1 (the API) works with a range of Feature Levels (the hardware). WARP on Windows 8 supports FL 11.0 (and 10.1 as before) and includes support for the DXGI 1.2 16bpp formats (565, 5551, 4444). The Windows 8 Developer Preview SDK includes the latest HLSL compiler FXC tool and D3DCompiler.DLL, the Debug Layers DLL, and the REF device DLL for DirectX 11.1 on Windows 8. The MSDN documentation now includes details on SM 4.x and SM 5.0 shader assembly (for deciphering the compiler’s disassembly output) plus details on BC6H/BC7 compression formats <http://msdn.microsoft.com/en-us/library/bb943998(v=VS.85).aspx> <http://msdn.microsoft.com/en-us/library/hh447232(v=VS.85).aspx> <http://msdn.microsoft.com/en-us/library/hh308955(v=VS.85).aspx> What is different from DirectX 11 on PC
The upgrade from DirectX 11 to DirectX 11.1 is targeting the following areas:
- Enabling Metro-style applications (there’s some additional access control for this which impacted almost every API in the OS so there’s no Direct3D 9 in Metro-style, but Direct3D 11.x is fully supported)
- Technical computing (optional extended double-precision instructions (division, etc.) and optional Sum of Absolute Differences instruction; enabling hardware access via Direct3D from session 0; HLSL compiler improvements)
- Low-power device optimizations (reduced shader precision hints for HLSL/driver, Tiled Graphics Rendering optimizations, 4 bit-per-pixel DXGI formats 565, 5551, 4444)
- Various graphics stack unification efforts (Direct3D 11 Video, Direct3D interop improvements for Direct2D & Media Foundation, etc.)
- Windows on ARM
1. Use UAV's at every Pipeline stage
2. Use logical operations in a render target
3. Shader tracing: looks like a new way to measure shader performance
The functions (ID3D11Device::CheckFeatureSupport / ID3D11Device::CheckFormatSupport) that check for supported features and formats were extended as well. D3D11_FEATURE_DATA_ARCHITECTURE_INFO seems to be for tiled-based rendering hardware commonly used in mobile GPUs and D3D11_FEATURE_DATA_SHADER_MIN_PRECISION_SUPPORT too. DXGI_FORMAT was extended to support video formats that now can be processed with shaders by using resource views (SRV/RTV/UAV). There is a new D3D_FEATURE_LEVEL_11_1 defined (i.e. a minor revision of the hardware feature set), but I don’t (yet) have a good link to give you to summarize the required features. Of course, there’s no public drivers or hardware out yet that exposes FL 11.1 anyhow. As before, DirectX 11.1 (the API) works with a range of Feature Levels (the hardware). WARP on Windows 8 supports FL 11.0 (and 10.1 as before) and includes support for the DXGI 1.2 16bpp formats (565, 5551, 4444). The Windows 8 Developer Preview SDK includes the latest HLSL compiler FXC tool and D3DCompiler.DLL, the Debug Layers DLL, and the REF device DLL for DirectX 11.1 on Windows 8. The MSDN documentation now includes details on SM 4.x and SM 5.0 shader assembly (for deciphering the compiler’s disassembly output) plus details on BC6H/BC7 compression formats <http://msdn.microsoft.com/en-us/library/bb943998(v=VS.85).aspx> <http://msdn.microsoft.com/en-us/library/hh447232(v=VS.85).aspx> <http://msdn.microsoft.com/en-us/library/hh308955(v=VS.85).aspx> What is different from DirectX 11 on PC
- D3DX9, D3DX10, D3DX11 are not supported for Metro-style applications.
- The Texconv sample includes the "DirectXTex" library which has all the texture processing functionality, WIC-based IO, DDS codec, BC software compression/decompression, etc. as shared source that was in D3DX11.
- D3DCSX_44.DLL is in the Windows SDK for redist with applications, and I believe is supported in Metro style applications.
- D3DCompiler_44.DLL is available for REDIST with Desktop applications and for development, but is not supported for REDIST in Metro-style applications. We've long recommended not doing run-time compliation, and Metro style enforces this at deployment time.
- XINPUT1_4.DLL and XAUDIO2_8.DLL are included in the OS and are fully supported for Metro style applications.
Sunday, July 31, 2011
Even Error-Distribution: Rules for Designing Graphics Sub-Systems (Part III)
The design rule of "Even Error-Distribution" is very common in everything we do as graphics/engine programmers. Compared to the "No Look-up Tables" and "Screen-Space" rules, it is probably easier to agree on this principle in general. The idea is that whatever technique you implement, you face the observer always with a consistent "error" level. The word error describes here a difference between what we consider the real world experience and the visual experience in a game. Obvious examples are toon and hatch shading, where we do not even try to render anything that resembles the real world but something that is considered beautiful. More complex examples are the penumbras of shadow maps, ambient occlusion or a real-time global illumination approach that has a rather low granularity.
The idea behind this design rule is that whatever you do, do it consistently and hope that the user will adjust to the error and not recognize it after a while anymore. Because the error is evenly distributed throughout your whole game, it is tolerated easier by the user.
To look at it from a different perspective. At Confetti we target most of the available gaming platforms. We can render very similar geometry and textures on different platforms. For example iOS/Android with OpenGL ES 2.0 and then Windows with DirecX 11 or XBOX 360 with its Direct3D. For iOS / Android you want to pick different lighting and shadowing techniques than for the higher end platforms. For shadows it might be stencil shadow volumes on low-end platforms and shadow maps on high end platforms. Those two shadowing techiques have very different performance and visual characteristics. The "error" resulting from stencil shadow volumes is that the shadows are -by default- very sharp and pronounced while shadow maps on the higher end platforms can be softer and more like real life shadows.
A user that watches the same game running on those platforms, will adjust to the "even" error of each of those shadow mapping techniques as long as they do not change on the fly. If you would mix the sharp and the soft shadows, users will complain that the shadow quality changes. If you provide only one or the other shadow, there is a high chance that people will just get used to the shadow appearance.
Similar ideas apply to all the graphics programming techniques we use. Light mapping might be a viable option on low end platforms and provide pixel perfect lighting, a dynamic solution replacing those light maps might have a higher error level and not being pixel perfect. As long as the lower quality version always looks consistent, there is a high chance that users won't complain. If we would change the quality level in-game, we are probably faced with reviews that say that the quality is changing.
Following this idea, one can exclude techniques that change the error level on the fly during game play. There were certainly a lot of shadow map techniques in the past that had different quality levels based on the angle between the camera and the sun. Although in many cases they looked better than the competing techniques, users perceived the cases when their quality was lowest as a problem.
Any technique based on re-projection, were the quality of shadows, Ambient Occlusion or Global Illumination changes while the user watches a scene, would violate the "Even Error-Distribution" rule.
A game that mixes light maps that hold shadow and/or light data and dynamic light and / or regular shadow maps might have the challenge to make sure that there is no visible difference between the light and shadow quality. Quite often the light mapped data looks better than the dynamic techniques and the experience is inconsistent. Evenly distributing the error into the light map data would increase the user experience because he/she is able to adjust better to an even error distribution. The same is true for any form of megatexture approach.
A common problem of mixing light mapped and generated light and shadow data is that in many cases dynamic objects like cars or characters do not receive the light mapped data. Users seems to have adjusted to the difference in quality here because it was consistent.
The idea behind this design rule is that whatever you do, do it consistently and hope that the user will adjust to the error and not recognize it after a while anymore. Because the error is evenly distributed throughout your whole game, it is tolerated easier by the user.
To look at it from a different perspective. At Confetti we target most of the available gaming platforms. We can render very similar geometry and textures on different platforms. For example iOS/Android with OpenGL ES 2.0 and then Windows with DirecX 11 or XBOX 360 with its Direct3D. For iOS / Android you want to pick different lighting and shadowing techniques than for the higher end platforms. For shadows it might be stencil shadow volumes on low-end platforms and shadow maps on high end platforms. Those two shadowing techiques have very different performance and visual characteristics. The "error" resulting from stencil shadow volumes is that the shadows are -by default- very sharp and pronounced while shadow maps on the higher end platforms can be softer and more like real life shadows.
A user that watches the same game running on those platforms, will adjust to the "even" error of each of those shadow mapping techniques as long as they do not change on the fly. If you would mix the sharp and the soft shadows, users will complain that the shadow quality changes. If you provide only one or the other shadow, there is a high chance that people will just get used to the shadow appearance.
Similar ideas apply to all the graphics programming techniques we use. Light mapping might be a viable option on low end platforms and provide pixel perfect lighting, a dynamic solution replacing those light maps might have a higher error level and not being pixel perfect. As long as the lower quality version always looks consistent, there is a high chance that users won't complain. If we would change the quality level in-game, we are probably faced with reviews that say that the quality is changing.
Following this idea, one can exclude techniques that change the error level on the fly during game play. There were certainly a lot of shadow map techniques in the past that had different quality levels based on the angle between the camera and the sun. Although in many cases they looked better than the competing techniques, users perceived the cases when their quality was lowest as a problem.
Any technique based on re-projection, were the quality of shadows, Ambient Occlusion or Global Illumination changes while the user watches a scene, would violate the "Even Error-Distribution" rule.
A game that mixes light maps that hold shadow and/or light data and dynamic light and / or regular shadow maps might have the challenge to make sure that there is no visible difference between the light and shadow quality. Quite often the light mapped data looks better than the dynamic techniques and the experience is inconsistent. Evenly distributing the error into the light map data would increase the user experience because he/she is able to adjust better to an even error distribution. The same is true for any form of megatexture approach.
A common problem of mixing light mapped and generated light and shadow data is that in many cases dynamic objects like cars or characters do not receive the light mapped data. Users seems to have adjusted to the difference in quality here because it was consistent.
Sunday, July 3, 2011
No Look-up Tables: Rules for Designing Graphics Sub-systems (Part II)
One of the design principles I apply to graphics systems nowadays is to avoid any look-up table. That means not only mathemetical look-up tables -the way we used them in the 80ieth and the 90ieth- but also cached lighting, shadow and other data, that is sometimes stored in light or radiosity maps.
This design principle follows the development of GPUs. While decent GPUs offer with each new iteration a larger number of arithetic instructions, the memory bandwidth is stagnating since several years. Additionally transporting data to the GPU might be slow due to several bottlenecks like DVD speed, PCI Express bus etc.. In many cases it might be more efficient to calculate a result with the help of arithmetic instructions, instead of doing a look-up in a texture or any other memory area. Saving streaming bandwidth throughout the hardware is also a good motivation to avoid look-up textures like this. Quite often any look-up technique doesn't allow a 24 hour game cycle, where the light and shadows have to move accordingly with time.
In many cases using pre-baked textures to store lighting, shadowing or other data also leads to a scenario where the geometry on which the texture is applied is not destructible anymore.
Typical examples are:
- Pre-calculating a lighting equation and storing results in a texture like a 2D, Cube or 3D map
- Large terrain textures, like megatextures. Texture synthesis might be more efficient here
- Light and radiosity maps and other pre-calculated data for Global illumination approaches
- Signed distance fields (if they don't allow 24 hour cycle lights and shadows)
- Voxels as long as they require a large amount of data to be re-read each frame and don't allow dynamic lighting and shadows (24 hour cycle)
- ... and more ...
Following the "No Look-up Table" design principle, one of the options to store intermediate data is to cache it in GPU memory, so that data doesn't need to be generated on the fly. This might be a good option depending on the amount of memory available on the GPU.
Depending on the underlying hardware platform or the requirements of the game, the choice between different caching schemes makes a system like this very flexible.
Here are a collection of ideas that might help to make an informed decision on when to apply a caching scheme, that keeps data around in GPU memory:
- Whenever the data is not visible to the user, it doesn't need to be generated. For example color, light and shadow data only need to be generated if the user can see them. That requires that they are on-screen with sufficient size. Projecting an object into screen-space allows to calculate its size. If it is too small or not visible any data attached to it doesn't need to be generated. This idea does not only apply to geometric objects but also light and shadows. If a shadow is too small on the screen, we do not have to re-generate it.
- Cascaded Shadow maps introduced a "level of shadowing" system that distributes shadow resolution along the view frustum in a way that the shadow resolution distribution dedicates less resolution to objects farer away, while closer up objects recieve relativly more shadow resolution. Similarly lighting quality should increase and decrease based on distance. Cascaded Reflective shadow maps extend the idea on any global illumination data, like one bounce diffuse lighting and ambient occlusion.
- If the quality requirements are rather low because the object is far away or small, screen-space techniques might allow to store data in a higher density. For example Screen-Space Global illumination approaches that are based on the G-Buffer - that is already used to apply Deferred Lights in a scene- can offer an efficient way to light far away objects.
This design principle follows the development of GPUs. While decent GPUs offer with each new iteration a larger number of arithetic instructions, the memory bandwidth is stagnating since several years. Additionally transporting data to the GPU might be slow due to several bottlenecks like DVD speed, PCI Express bus etc.. In many cases it might be more efficient to calculate a result with the help of arithmetic instructions, instead of doing a look-up in a texture or any other memory area. Saving streaming bandwidth throughout the hardware is also a good motivation to avoid look-up textures like this. Quite often any look-up technique doesn't allow a 24 hour game cycle, where the light and shadows have to move accordingly with time.
In many cases using pre-baked textures to store lighting, shadowing or other data also leads to a scenario where the geometry on which the texture is applied is not destructible anymore.
Typical examples are:
- Pre-calculating a lighting equation and storing results in a texture like a 2D, Cube or 3D map
- Large terrain textures, like megatextures. Texture synthesis might be more efficient here
- Light and radiosity maps and other pre-calculated data for Global illumination approaches
- Signed distance fields (if they don't allow 24 hour cycle lights and shadows)
- Voxels as long as they require a large amount of data to be re-read each frame and don't allow dynamic lighting and shadows (24 hour cycle)
- ... and more ...
Following the "No Look-up Table" design principle, one of the options to store intermediate data is to cache it in GPU memory, so that data doesn't need to be generated on the fly. This might be a good option depending on the amount of memory available on the GPU.
Depending on the underlying hardware platform or the requirements of the game, the choice between different caching schemes makes a system like this very flexible.
Here are a collection of ideas that might help to make an informed decision on when to apply a caching scheme, that keeps data around in GPU memory:
- Whenever the data is not visible to the user, it doesn't need to be generated. For example color, light and shadow data only need to be generated if the user can see them. That requires that they are on-screen with sufficient size. Projecting an object into screen-space allows to calculate its size. If it is too small or not visible any data attached to it doesn't need to be generated. This idea does not only apply to geometric objects but also light and shadows. If a shadow is too small on the screen, we do not have to re-generate it.
- Cascaded Shadow maps introduced a "level of shadowing" system that distributes shadow resolution along the view frustum in a way that the shadow resolution distribution dedicates less resolution to objects farer away, while closer up objects recieve relativly more shadow resolution. Similarly lighting quality should increase and decrease based on distance. Cascaded Reflective shadow maps extend the idea on any global illumination data, like one bounce diffuse lighting and ambient occlusion.
- If the quality requirements are rather low because the object is far away or small, screen-space techniques might allow to store data in a higher density. For example Screen-Space Global illumination approaches that are based on the G-Buffer - that is already used to apply Deferred Lights in a scene- can offer an efficient way to light far away objects.
Monday, June 13, 2011
Screen-Space: Rules for Designing Graphics Sub-systems (Part I)
Since programming GPUs allow one to design more complex graphics systems, I started to develop a few simple rules that have survived the test of time, while designing graphics sub-systems like Skydome, PostFX, Vegetation, Particle, Global Illumination, Light & Shadow systems etc..
Here are three of them:
1. Screen-Space (Part I - this part)
2. No Look-up Tables (Part II)
3. Even Error Distribution (Part III)
Today we focus on the Screen-Space design rule. It says: "do everything you can in Screen-Space because it is more efficient most of the time". This is easy to say for the wide range of effects that are part of a Post-Processing Pipeline like Depth of Field, Motion Blur, Tone Mapping and color filters, light streaks and others (read more in [Engel07]), as well as anti-aliasing techniques like MLAA that anti-alias the image in screen-space.
With the increased number of arithmetic instructions available and the stagnating growth of memory bandwidth, two new groups of sub-systems can be moved into screen-space.
Accompanying Deferred Lighting systems, more expensive materials like skin and hair can now be applied in screen-space; this way a screen-space material system is possible [Engel], solving some of the bigger challenges to implementing a Deferred Lighting pipeline.
Global Illumination and Shadow filter kernels can be moved into screen-space as well. For example, for a large number of Point or Ellipsoidal Shadow Maps, all the shadow data can be stored in a shadow collector in screen-space and then an expensive filter kernel can be applied to this screen-space texture [Engel2010].
The wide range of abilities available with screen-space filter kernels makes it valuable to look at the challenges while implementing them in general. The common challenges to applying materials or lights and shadows with the help of large-scale filter kernels in screen-space are mostly:
1. Scale filter kernel based on camera distance
2. Add anisotropic "behavior" to the screen-space filter kernel
3. Restricting the filter kernel based on the Z value of the Tap
Scaling Filter Kernel based on Camera Distance
Using a screen-space filter kernel for filtering shadows, GI, emulating sub-surface scattering for skin or rendering hair, requires at some point to scale the filter kernel based on the distance from the camera or, better yet, the near plane to the pixel in question. What has worked in the past is:
Anisotropic Screen-Space Filter Kernel
Following [Geusebroek], anisotropy can be added to a screen-space filter kernel by projecting into a ellipse following the orientation of the geometry.

Image 1 - Anisotropic Screen-Space Filter Kernel
Normals that are stored in a world-space buffer in a G-Buffer can be compared to the view vector. The elliptical "response" is achieved by taking the square root of this operation.
Restricting the filter kernel based on the Z value of the Tap
One of the challenges with any screen-space filter kernel is the fact that the wide filter kernel can smear values into the penumbra around "corners" of geometry (read more in [Gumbau].

Image 2 - Error introduced by running a large filter kernel in screen-space
A common way to solve this problem is to compare the depth values of the center of the filter kernel with the depth values of the filter kernel taps and define a certain threshold where we consider the difference between the depth values large enough to early out. A source code snippet for this might look like this.
I would like to thank Carlos Dominguez for the discussions about how to scale filter kernels based on camera distance.
References
[Engel] Wolfgang Engel, "Deferred Lighting / Shadows / Materials", FMX 2011, http://www.confettispecialfx.com/confetti-on-fmx-in-stuttgart-ii
[Engel07] Wolfgang Engel, "Post-Processing Pipeline", GDC 2007, http://www.coretechniques.info/index_2007.html
[Engel2010] Wolfgang Engel, "Massive Point Light Soft Shadows", http://www.confettispecialfx.com/massive-point-light-soft-shadows
[Geusebroek] Jan-Mark Geusebroek, Arnold W. M. Smeulders, J. van de Weijer, “Fast anisotropic Gauss filtering”, IEEE Transactions on Image Processing, Volume 12 (8), page 938-943, 2003
[Gilham] David Gilham, "Real-Time Depth-of-Field Implemented with a Post-Processing only Technique", ShaderX5: Advanced Rendering, Charles River Media / Thomson, pp 163 - 175, ISBN 1-58450-499-4
[Gumbau] Jesus Gumbau, Miguel Chover, and Mateu Sbert, “Screen-Space Soft Shadows”, GPU Pro, pp. 477 - 490
Here are three of them:
1. Screen-Space (Part I - this part)
2. No Look-up Tables (Part II)
3. Even Error Distribution (Part III)
Today we focus on the Screen-Space design rule. It says: "do everything you can in Screen-Space because it is more efficient most of the time". This is easy to say for the wide range of effects that are part of a Post-Processing Pipeline like Depth of Field, Motion Blur, Tone Mapping and color filters, light streaks and others (read more in [Engel07]), as well as anti-aliasing techniques like MLAA that anti-alias the image in screen-space.
With the increased number of arithmetic instructions available and the stagnating growth of memory bandwidth, two new groups of sub-systems can be moved into screen-space.
Accompanying Deferred Lighting systems, more expensive materials like skin and hair can now be applied in screen-space; this way a screen-space material system is possible [Engel], solving some of the bigger challenges to implementing a Deferred Lighting pipeline.
Global Illumination and Shadow filter kernels can be moved into screen-space as well. For example, for a large number of Point or Ellipsoidal Shadow Maps, all the shadow data can be stored in a shadow collector in screen-space and then an expensive filter kernel can be applied to this screen-space texture [Engel2010].
The wide range of abilities available with screen-space filter kernels makes it valuable to look at the challenges while implementing them in general. The common challenges to applying materials or lights and shadows with the help of large-scale filter kernels in screen-space are mostly:
1. Scale filter kernel based on camera distance
2. Add anisotropic "behavior" to the screen-space filter kernel
3. Restricting the filter kernel based on the Z value of the Tap
Scaling Filter Kernel based on Camera Distance
Using a screen-space filter kernel for filtering shadows, GI, emulating sub-surface scattering for skin or rendering hair, requires at some point to scale the filter kernel based on the distance from the camera or, better yet, the near plane to the pixel in question. What has worked in the past is:
// linear depth read more in [Gilham]
// Q = FarClip / (FarClip – NearClip)
// Depth = value from a hyperbolic depth buffer
float depthLin= (-NearClip * Q) / (Depth - Q);// scale based on distance to the viewer
// renderer->setShaderConstant4f("TexelSize", vec4(width, height, 1.0f / width, width / height));
sampleStep.xy = float2(1.0f, TexelSize.w) * sqrt(1.0f / ((depthLin.xx * depthLin.xx) * bias));Scaling only happens based on linearized depth values that are going from 0.0..1.0 between the near and far plane. This considers the camera's near and far plane settings. The bias value is a user defined "magic" value. The last channel in the TexelSize variable holds the x and y direction ratio of the pixel. The inner term - 1.0/distance2- of the equation resembles a simple light attenuation function. We will improve this equation in the near future.Anisotropic Screen-Space Filter Kernel
Following [Geusebroek], anisotropy can be added to a screen-space filter kernel by projecting into a ellipse following the orientation of the geometry.

Image 1 - Anisotropic Screen-Space Filter Kernel
Normals that are stored in a world-space buffer in a G-Buffer can be compared to the view vector. The elliptical "response" is achieved by taking the square root of this operation.
float Aniso = saturate(sqrt(dot( viewVec, normal )));Restricting the filter kernel based on the Z value of the Tap
One of the challenges with any screen-space filter kernel is the fact that the wide filter kernel can smear values into the penumbra around "corners" of geometry (read more in [Gumbau].

Image 2 - Error introduced by running a large filter kernel in screen-space
A common way to solve this problem is to compare the depth values of the center of the filter kernel with the depth values of the filter kernel taps and define a certain threshold where we consider the difference between the depth values large enough to early out. A source code snippet for this might look like this.
bool isValidSample = bool( abs(sampleDepth - d) < errDepth );
if (isValidSample && isShadow)
{
// the sample is considered valid
sumWeightsOK += weights[i+1]; // accumulate valid weights
Shadow += sampleL0.x * weights[i+1]; // accumulate weighted shadow value
}AcknowledgementsI would like to thank Carlos Dominguez for the discussions about how to scale filter kernels based on camera distance.
References
[Engel] Wolfgang Engel, "Deferred Lighting / Shadows / Materials", FMX 2011, http://www.confettispecialfx.com/confetti-on-fmx-in-stuttgart-ii
[Engel07] Wolfgang Engel, "Post-Processing Pipeline", GDC 2007, http://www.coretechniques.info/index_2007.html
[Engel2010] Wolfgang Engel, "Massive Point Light Soft Shadows", http://www.confettispecialfx.com/massive-point-light-soft-shadows
[Geusebroek] Jan-Mark Geusebroek, Arnold W. M. Smeulders, J. van de Weijer, “Fast anisotropic Gauss filtering”, IEEE Transactions on Image Processing, Volume 12 (8), page 938-943, 2003
[Gilham] David Gilham, "Real-Time Depth-of-Field Implemented with a Post-Processing only Technique", ShaderX5: Advanced Rendering, Charles River Media / Thomson, pp 163 - 175, ISBN 1-58450-499-4
[Gumbau] Jesus Gumbau, Miguel Chover, and Mateu Sbert, “Screen-Space Soft Shadows”, GPU Pro, pp. 477 - 490
Sunday, May 29, 2011
Points, Vertices and Vectors
This post covers some facts about Points, Vertices and Vectors that might be useful. This is a collection of ideas to create a short math primer for engineers that want to explore computer graphics. The resulting material will be used in future computer graphics classes. Your feedback is highly welcome!
Points
A 3D point is a location in space, in a 3D coordinate system. We can find a point P with coordinates [Px, Py, Pz] by starting from the origin at [0, 0, 0] and moving the distance Px, Py and Pz along the x, y and z axis.
Two points define a line segment between them, three points define a triangle with corners at those points, and several interconnected triangles can be used to define the surface of an object; sometimes also called mesh.
Points that are used to define geometric entities like triangles, are often called vertices. In graphics programming, vertices are an array of structures or a structure of arrays and not only describe a position but also include other data like for example color, a normal vector or texture coordinates.
The difference of two points is a vector: V = P - Q
Vectors
While a point is a reference to a location, a vector is the difference between two points which describes a direction and a distance -length-, or a displacement.
Like points, vectors can be represented by three coordinates. Those three values are retrieved by subtracting the tail from the vector from its head.
Δx = (xh - xt)
Δy = (yh - yt)
Δz = (zh - zt)

Figure 1 - Vector components Δx, Δy and Δz
Two vectors are equal if they have the same values. Thus considering a value as a difference of two points, there are any number of vectors with the same direction and length.

Figure 2 - Instances of one vector
The difference between between points and vectors is reiterated by saying they live in a different space, the Euclidean space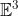 and the vector space
and the vector space 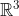 . Read more in [Farin].
. Read more in [Farin].
The primary reason for differentiating between points and vectors is to achieve geometric constructions which are coordinate independent. Such constructions are manipulations applied to objects that produce the same result regardless of the location of the coordinate origin.
Scalar Multiplication, Addition and Subtraction of Vectors
A vector V can be multiplied by a scalar. Multiplying by 2 doubles the vectors components.

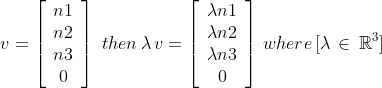
Similarly dividing the vector by 2 halves its components. The direction of the vector remains unchanged, only its magnitude changes.
The result of adding two vectors V and W can be obtained geometrically.

Figure 3 - Adding two vectors
Placing the tail of w to the head of V leads to the resulting vector, going from V's tail to W's head. In a similar manner vector subtraction can visualized.

Figure 4 - Subtracting two vectors
Similar to addition, the tail of the vector that should be subtracted -W- is placed to the head of V. Then the vector that should be subtracted is negated. The resulting vector runs from V's tail to W's head.
Alternatively, by the parallelogram law, the vector sum can be seen as the diagonal of the parallelogram formed by the two vectors.

Figure 5 - Parallelogram rule
The vectors V - W and V + W are the diagonals of the parallelogram defined by V and W. Arithmetically, vectors are added or subtracted by adding or subtracting the components of each vector.
All the vector additions and subtractions are coordinate independent operations, since vectors are defined as difference of points.
Homogeneous Coordinates
Representing both points and vectors with three coordinates can be confusing. Homogeneous coordinates are a useful tool to make the distinction explicit. Adding a fourth coordinate, named w, allows us to describe a direction or a vector by setting this coordinate to 0. In all other cases we have a point or location.
Dividing a homogeneous point [Px, Py, Pz, Pw] by the w component leads to the corresponding 3D point. If the w component equals to zero, the point would be infinitely far away, which is then interpreted as a direction. Using any non-zero value for w, will lead to points all corresponding to the same 3D point. For example the point (3, 4, 5) has homogeneous coordinates (6, 8, 10, 2) or (12, 16, 20, 4).
The reason why this coordinate system is called "homogeneous" is because it is possible to transform functions f(x, y, z) into the form f(x/w, y/w, z/w) without disturbing the degree of the curve. This is useful in the field of projective geometry. For example a collection of 2D homogeneous points (x/t, y/t, t) exist on a xy-plane where t is the z-coordinate as illustrated in figure 6.

Figure 6 - 2D homogenous coodinates can be visualized as a plane in 3D space
Figure 6 shows a triangle on the t = 1 plane, and a similar triangle much larger on a distant plane. This creates an arbitrary xy plane in three dimensions. The t- or z-coordinate of the plane is immaterial because the x- and y-coordinates are eventually scaled by t.
Homogeneous coordinates are also used to create a translation transform.
In game development, some math libraries have dedicated point and vector classes. The main distinction is made by setting the fourth channel to zero for vectors and one for points [Eberly].
Pythagorean Theorem
The length or magnitude of a vector can be obtained by applying the Pythagorean Theorem. The opposite -b- and adjacent -a- side of a right-angled triangle represents orthogonal directions. The hypotenuse is the shortest path distance between those.
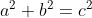

Figure 7 - Pythagorean Theorem
It helps thinking of the Pythagorean Theorem as a tool to compare "things" moving at right angles. For example if a is 3, b equals 4, then c equals 5 [Azad].
The Pythagorean Theorem can also be applied to right-angled triangles chained together.

Figure 8 - Pythagorean Theorem with two triangles chained together
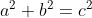
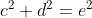
Replacing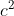 with
with 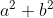 leads to
leads to
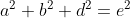
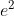 is now written in three orthogonal components. Instead of lining the triangles flat, we can now tilt the green one a bit and therefore consider an additional dimension.
is now written in three orthogonal components. Instead of lining the triangles flat, we can now tilt the green one a bit and therefore consider an additional dimension.

Figure 9 - Pythagorean Theorem in 3D
Renaming the sides to x, y and z instead of a, b and d we get:
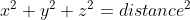
This works with any number of dimensions.
The Pythagorean Theorem is the basis for computing distance between two points. Consider the following two triangles:

Figure 10 - Pythagorean Theorem used for distance calculations
The distance from the tip of the blue triangle at coordinate (4, 3) to the tip of the green triangle at coordinate (8, 5) can be calculated by creating a virtual triangle between those points. Subtracting the points leads to a 2D vector.
Δx = (xhead - xtail)
Δy = (yhead - ytail)
}^2} + {{(\Delta y)}^2}}})
In this case
Δx = 8 - 4 = 4
Δy = 5 - 3 = 2
}^2} + {{(2)}^2}}})
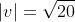
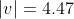
Extending the idea to three dimensions shows the well-known equation:
}^2} + {{(\Delta y)}^2 + {{(\Delta z)}^2}}})
Unit Vectors
A unit vector has a length or magnitude of 1. This is a useful property for vector multiplications, because those consider the magnitude of a vector and the computation time can be reduced if this magnitude is one (more on this later). A unit column vector might look like this:
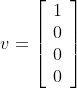
and
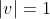
Converting a vector into a unit form is called normalizing and is achieved by dividing a vector's components by its magnitude. Its magnitude is retrieved by applying the Pythagorean Theorem.
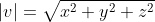
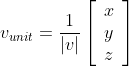
An example might be:
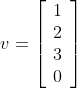
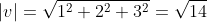

Cartesian Unit Vectors
Now that we have investigated the scalar multiplication of vectors, vector addition and subtraction and unit vectors, we can combine those to permit the algebraic manipulation of vectors (read more at [Vince][Lengyel]). A tool that helps to achieve this is called Cartesian unit vectors. The three Cartesian unit vectors i, j and k are aligned with the x-, y- and z-axes.
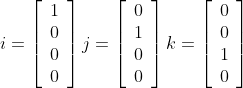
Any vector aligned with the x-, y- and z-axes can be defined by a scalar multiple of the unit vectors i, j and k. For example a vector 15 units long aligned with the y-axis is simply 15j. A vector 25 units long aligned with the z axis is 25k.
By employing the rules of vector addition and subtraction, we can compose a vector R by summing three Cartesian unit vectors as follows.
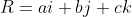
This is equivalent to writing R as
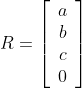
The magnitude of R would then be computed as
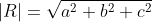
Any pair of Cartesian vectors such as R and S can be combined as follows
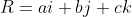
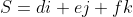
i + (b \pm e)j + (c \pm f)k)
An example would be
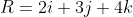
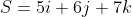
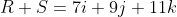
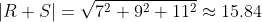
Vector Multiplication
Vector multiplication provides some powerful ways of computing angles and surface orientations. While the multiplication of two scalars is a familiar operation, the multiplication of vectors is a multiplication of two 3D lines, which is not an easy operation to visualize. In vector analysis, there are generally two ways to multiply vectors: one results in a scalar value and the other one in a vector.
Scalar or Dot Product
Multiplying the magnitude of two vectors |R| and |S| is a valid operation but it ignores the orientation of the vectors, which is one of their important features. Therefore we want to include the angles between the vectors. In case of the scalar product, this is done by projecting one vector onto the other.

Figure 11 - Projecting R on S
The projection of R on S creates the basis for the scalar product, because it takes into account their relative orientation. The length of R on S is
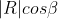
Then we can multiply the projected length of R with the magnitude of S
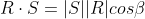
or commonly written
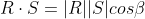
The symbol is used to represent scalar multiplications and to distinguish it from the vector product, which employs the
symbol is used to represent scalar multiplications and to distinguish it from the vector product, which employs the 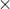 symbol. Because of this symbol, the scalar product is often referred to as the dot product. This geometric interpretation of the scalar product shows that in case the magnitude of R and S is one -in other words they are unit vectors- the calculation of the scalar product only relies on
symbol. Because of this symbol, the scalar product is often referred to as the dot product. This geometric interpretation of the scalar product shows that in case the magnitude of R and S is one -in other words they are unit vectors- the calculation of the scalar product only relies on 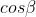 . The following figure shows a number of dot product scenarios.
. The following figure shows a number of dot product scenarios.

Figure 12 - Dot product
The geometric representation of the dot product is useful to imagine how it works but it doesn't map well to computer hardware. The algebraic representation maps better to computer hardware and is calculated with the help of Cartesian components:
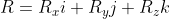
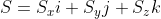
 \cdot (S_xi + S_yj + S_zk) \\ = R_xi \cdot (S_xi + S_yj + S_zk) + R_yi \cdot (S_xi + S_yj + S_zk) + R_zi \cdot (S_xi + S_yj + S_zk))

There are various dot product terms such as etc. in this equation. With the help of the geometric representation of the dot product it can be determined that terms that are mutually perpendicular like
etc. in this equation. With the help of the geometric representation of the dot product it can be determined that terms that are mutually perpendicular like  are zero because the cosinus of 90 degrees is zero. This leads to
are zero because the cosinus of 90 degrees is zero. This leads to
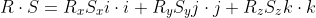
Finally, terms with two vectors that are parallel to themselve lead to a value of one because the cosinus of a degree of zero is one. Additionally the Cartesian vectors are all unit vectors, which leads to
= 1)
So we end up with the familiar equation
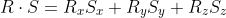
An example:
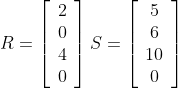
The algebraic representation results in:
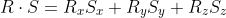

The geometric representation starts out with:
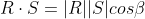
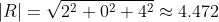
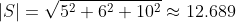
Solving for the angle between the vectors by plugging in the result of the algebraic representation:


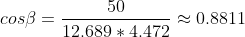
Solving for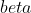 leads to the angle between the two vectors:
leads to the angle between the two vectors:
 \approx 28.22^\circ)
The resulting angle will be always between and
and  , because, as the angle between two vectors increases beyond
, because, as the angle between two vectors increases beyond  the returned angle
the returned angle  is always the smallest angle associated with the geometry.
is always the smallest angle associated with the geometry.
Scalar Product in Lighting Calculations
Many games utilize the Blinn-Phong lighting model (see Wikipedia; ignore the code on this page). A part of the diffuse component of this lighting model is the Lambert's Law term published in 1760. Lambert stated that the intensity of illumination on a diffuse surface is proportional to the cosine of the angle between the surface normal vector and the light source direction.
Let's assume our light source is located in our reference space for lighting at (20, 30, 40), while our normal vector is normalized and located at (0, 11, 0). The point where the intensity of illumination is measured is located at (0, 10, 0).

Figure 13 - Lighting Calculation
The light and normal vector are calculated by subtracting the position of the point where the intensity is measured -representing their tails- from their heads.
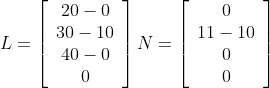

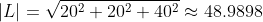
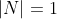
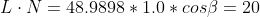
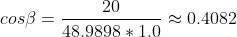
Instead of using the original light vector, the following scalar product normalizes the light vector first, before using it in the lighting equation.
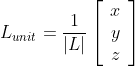

To test if the light vectors magnitude is one:
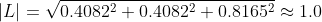
Plugging the unit light vector and the unit normal vector into the algebraic representation of the scalar product.

Now solving the geometrical representation for the cosine of the angle.
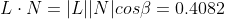
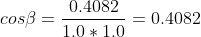
In case the light and the normal vector are unit vectors, the result of the algebraic scalar product calculation equals the cosinus of the angle. The algebraic scalar product is implemented in the dot product intrinsic available for the CPU and GPU. In other words, in case the involved vectors are unit vectors, a processor can calculate the cosine of the angle faster. This is the reason why normalized vectors might be more efficient in programming computer hardware.
Following Lambert's law, the intensity of illumination on a diffuse surface is proportional to the consine of the angle between the surface normal and the light source direction. That means that the point at (0, 10, 0) receives about 0.4082 of the original light intensity at (20, 30, 40) (attenuation is not considered in this example).
Coming back to image 12, in case, the unit light vector would have a y component that is one or minus one and therefore its x and y component would be zero, it would point in the same or opposite direction as the normal and therefore the last equation would result in one or minus one. If the unit light vector would have a z or x component equaling to one and therefore the other components would be zero, those equations would result in zero.
The Vector Product
Like the scalar product, the vector or cross product depends on the modulus of two vectors and the angle between them, but the result of the vector product is essentially different: it is another vector, at right angles to both the original vectors.
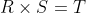
and
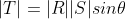
For an understanding of the vector product R and S, it helps to imagine a plane through those two vectors as shown in figure 14.

Figure 14 - Vector Product
The angle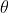 between the directions of the vectors suffices
between the directions of the vectors suffices 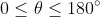 . There are two possible choices for the direction of the vector, each the negation of the other; the one chosen here is determined by the right-hand rule. Hold your right hand so that your forefinger points forward, your middle finger points out to the left, and your thumb points up. If you roughly align your forefinger with R, and your middle finger with S, then the cross product will point in the direction of your thumb.
. There are two possible choices for the direction of the vector, each the negation of the other; the one chosen here is determined by the right-hand rule. Hold your right hand so that your forefinger points forward, your middle finger points out to the left, and your thumb points up. If you roughly align your forefinger with R, and your middle finger with S, then the cross product will point in the direction of your thumb.

Figure 15 - Right-Hand rule Vector Product
The resulting vector of the cross product is perpendicular to R and S, that is
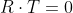
and
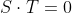
This makes the vector product an ideal way of computing normals. The two vectors R and S can be orthogonal but do not have to be. A property of the vector product that will be covered later is, that the magnitude of T is the area of the parallelogram defined by R and S.
Let's multiply two vectors together using the vector product.
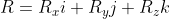
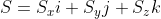
 \times (S_xi + S_yj + S_zk) \\ = R_xi \times (S_xi + S_yj + S_zk) + R_yi \times (S_xi + S_yj + S_zk) + R_zi \times (S_xi + S_yj + S_zk))

There are various vector product terms such as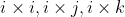 etc. in this equation. The terms
etc. in this equation. The terms 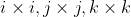 will result in a vector whose magnitude is zero, because the angle between those vectors is
will result in a vector whose magnitude is zero, because the angle between those vectors is  , and sin
, and sin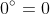 . This leaves
. This leaves

The other products between the unit vectors can be reasoned as:
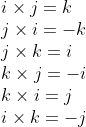
Those results show, that the commutative multiplication law is not applicable to vector products. In other words

Applying those findings reduces the vector product term to

Now re-grouping the equation to bring like terms together leads to:
i + (R_zS_x - R_xS_z)j + (R_xS_y - R_yS_x)k)
To achieve a visual pattern for remembering the vector product, some authors reverse the sign of the j scalar term.
i - (R_xS_z - R_zS_x)j + (R_xS_y - R_yS_x)k)
Re-writing the vector product as determinants might help to memorize it as well.
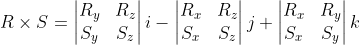
A 2x2 determinant is the difference between the product of the diagonal terms. With determinants a "recipe" for a vector product consists of the following steps:
1. Write the two vectors that should be multiplied as Cartesian vectors
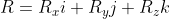
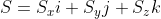
2. Write the cross product of those two vectors in determinant form, if this helps to memorize the process; otherwise skip to step 3.
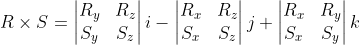
3. Then compute by plugging in the numbers into
i - (R_xS_z - R_zS_x)j + (R_xS_y - R_yS_x)k)
A simple example of a vector product calculation is to show that the assumptions that were made above, while simplifying the vector product, hold up.
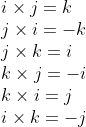
To show that there is a sign reversal when the vectors are reversed , let's calculate the cross product of those terms.
, let's calculate the cross product of those terms.
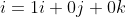
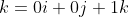
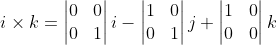
i - (1 * 1 - 0 * 0)j + (1 * 0 - 0 * 0)k)
The i and k terms are both zero, but the j term is -1, which makes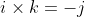 . Now reversing the vector product
. Now reversing the vector product
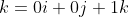
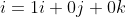
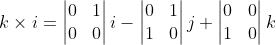
i - (0 * 0 - 1 * 1)j + (0 * 0 - 0 * 1)k)
Which shows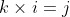
Deriving a Unit Normal Vector for a Triangle
Image 16 shows a triangle with vertices defined in anti-clockwise order. The side pointing towards the viewer is defined as the visible side in this scene. That means that the normal is expected to point roughly in the direction of where the viewer is located.

Figure 16 - Deriving a Unit Normal Vector
The vertices of the triangle are:
P1 (0, 2, 1)
P2 (0, 1, 4)
P3 (2, 0, 1)
The two vectors R and S are retrieved by subtracting the vertex at the head from the vertex at its tail.
Δx = (xh - xt)
Δy = (yh - yt)
Δz = (zh - zt)
Bringing the result into the Cartesian form
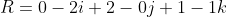
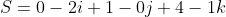
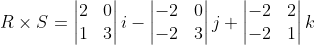
i - (-2 * 3 - 0 * -2)j + (-2 * 1 - 2 * -2)k)
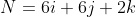
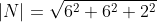
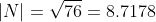
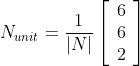
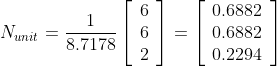
It is a common mistake to believe that if R and S are unit vectors, the cross product will also be a unit vector. The vector product equation shows that this is only true when the angle between the two vectors is 90 degrees and therefore the sinus of the angle theta is 1.
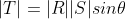
Please read in [Van Verth] about CPU implementation details.
Areas
The vector product might be used to determine the area of a parallelogram or a triangle (with the vertices at P1 - P3). Image 17 shows the two vectors helping to form a parallelogram and a triangle.

Figure 17 - Deriving the Area of a Parallelogramm / Triangle with the Vector Product
The height h is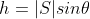 , therefore the area of the parallelogram is
, therefore the area of the parallelogram is
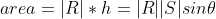
This equals the magnitude of the cross product vector T. Thus when we calculate the vector product of R and S, the length of the normal vector equals the area of the parallelogram formed by those vectors. The triangle forms half of the parallelogram and therefore half of the area.
area of parallelogram =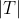
area of triangle =
or
area of triangle =
To compute the surface area of a mesh constructed from triangles or parallelograms, the magnitude of its non-normalized normals can be used like this.

The sign of the magnitude of the normal shows if the vertices are clockwise or counter-clockwise oriented.
References
[Azad] Kalid Azad, "Math Better Eplained", http://betterexplained.com/articles/math-betterexplained-ebook-available/
[Eberly] David H. Eberly, "3D Game Engine Design", p. 15, 2nd Edition, Morgan Kauffman 2007
[Farin] Gerald Farin, Dianne Hansford, "The Geometry Toolbox - For Graphics and Modeling", p. 16, AK Peters 1998
[Lengyel] Eric Lengyel, Mathematics for 3D Game Programming and Computer Graphics, Second Edition, Charles River Media 2003
[Vince] John Vince, "Mathematics for Computer Graphics", Springer, 3rd Edition, 2010
[Van Verth] James M. Van Verth, Lars M. Bishop, "Essential Mathematics for Games & Interactive Applications - A Programmer's Guide", Morgan Kaufmann 2004
Points
A 3D point is a location in space, in a 3D coordinate system. We can find a point P with coordinates [Px, Py, Pz] by starting from the origin at [0, 0, 0] and moving the distance Px, Py and Pz along the x, y and z axis.
Two points define a line segment between them, three points define a triangle with corners at those points, and several interconnected triangles can be used to define the surface of an object; sometimes also called mesh.
Points that are used to define geometric entities like triangles, are often called vertices. In graphics programming, vertices are an array of structures or a structure of arrays and not only describe a position but also include other data like for example color, a normal vector or texture coordinates.
The difference of two points is a vector: V = P - Q
Vectors
While a point is a reference to a location, a vector is the difference between two points which describes a direction and a distance -length-, or a displacement.
Like points, vectors can be represented by three coordinates. Those three values are retrieved by subtracting the tail from the vector from its head.
Δx = (xh - xt)
Δy = (yh - yt)
Δz = (zh - zt)

Figure 1 - Vector components Δx, Δy and Δz
Two vectors are equal if they have the same values. Thus considering a value as a difference of two points, there are any number of vectors with the same direction and length.

Figure 2 - Instances of one vector
The difference between between points and vectors is reiterated by saying they live in a different space, the Euclidean space
The primary reason for differentiating between points and vectors is to achieve geometric constructions which are coordinate independent. Such constructions are manipulations applied to objects that produce the same result regardless of the location of the coordinate origin.
Scalar Multiplication, Addition and Subtraction of Vectors
A vector V can be multiplied by a scalar. Multiplying by 2 doubles the vectors components.
Similarly dividing the vector by 2 halves its components. The direction of the vector remains unchanged, only its magnitude changes.
The result of adding two vectors V and W can be obtained geometrically.

Figure 3 - Adding two vectors
Placing the tail of w to the head of V leads to the resulting vector, going from V's tail to W's head. In a similar manner vector subtraction can visualized.

Figure 4 - Subtracting two vectors
Similar to addition, the tail of the vector that should be subtracted -W- is placed to the head of V. Then the vector that should be subtracted is negated. The resulting vector runs from V's tail to W's head.
Alternatively, by the parallelogram law, the vector sum can be seen as the diagonal of the parallelogram formed by the two vectors.

Figure 5 - Parallelogram rule
The vectors V - W and V + W are the diagonals of the parallelogram defined by V and W. Arithmetically, vectors are added or subtracted by adding or subtracting the components of each vector.
All the vector additions and subtractions are coordinate independent operations, since vectors are defined as difference of points.
Homogeneous Coordinates
Representing both points and vectors with three coordinates can be confusing. Homogeneous coordinates are a useful tool to make the distinction explicit. Adding a fourth coordinate, named w, allows us to describe a direction or a vector by setting this coordinate to 0. In all other cases we have a point or location.
Dividing a homogeneous point [Px, Py, Pz, Pw] by the w component leads to the corresponding 3D point. If the w component equals to zero, the point would be infinitely far away, which is then interpreted as a direction. Using any non-zero value for w, will lead to points all corresponding to the same 3D point. For example the point (3, 4, 5) has homogeneous coordinates (6, 8, 10, 2) or (12, 16, 20, 4).
The reason why this coordinate system is called "homogeneous" is because it is possible to transform functions f(x, y, z) into the form f(x/w, y/w, z/w) without disturbing the degree of the curve. This is useful in the field of projective geometry. For example a collection of 2D homogeneous points (x/t, y/t, t) exist on a xy-plane where t is the z-coordinate as illustrated in figure 6.

Figure 6 - 2D homogenous coodinates can be visualized as a plane in 3D space
Figure 6 shows a triangle on the t = 1 plane, and a similar triangle much larger on a distant plane. This creates an arbitrary xy plane in three dimensions. The t- or z-coordinate of the plane is immaterial because the x- and y-coordinates are eventually scaled by t.
Homogeneous coordinates are also used to create a translation transform.
In game development, some math libraries have dedicated point and vector classes. The main distinction is made by setting the fourth channel to zero for vectors and one for points [Eberly].
Pythagorean Theorem
The length or magnitude of a vector can be obtained by applying the Pythagorean Theorem. The opposite -b- and adjacent -a- side of a right-angled triangle represents orthogonal directions. The hypotenuse is the shortest path distance between those.

Figure 7 - Pythagorean Theorem
It helps thinking of the Pythagorean Theorem as a tool to compare "things" moving at right angles. For example if a is 3, b equals 4, then c equals 5 [Azad].
The Pythagorean Theorem can also be applied to right-angled triangles chained together.

Figure 8 - Pythagorean Theorem with two triangles chained together
Replacing

Figure 9 - Pythagorean Theorem in 3D
Renaming the sides to x, y and z instead of a, b and d we get:
This works with any number of dimensions.
The Pythagorean Theorem is the basis for computing distance between two points. Consider the following two triangles:

Figure 10 - Pythagorean Theorem used for distance calculations
The distance from the tip of the blue triangle at coordinate (4, 3) to the tip of the green triangle at coordinate (8, 5) can be calculated by creating a virtual triangle between those points. Subtracting the points leads to a 2D vector.
Δx = (xhead - xtail)
Δy = (yhead - ytail)
In this case
Δx = 8 - 4 = 4
Δy = 5 - 3 = 2
Extending the idea to three dimensions shows the well-known equation:
Unit Vectors
A unit vector has a length or magnitude of 1. This is a useful property for vector multiplications, because those consider the magnitude of a vector and the computation time can be reduced if this magnitude is one (more on this later). A unit column vector might look like this:
and
Converting a vector into a unit form is called normalizing and is achieved by dividing a vector's components by its magnitude. Its magnitude is retrieved by applying the Pythagorean Theorem.
An example might be:
Cartesian Unit Vectors
Now that we have investigated the scalar multiplication of vectors, vector addition and subtraction and unit vectors, we can combine those to permit the algebraic manipulation of vectors (read more at [Vince][Lengyel]). A tool that helps to achieve this is called Cartesian unit vectors. The three Cartesian unit vectors i, j and k are aligned with the x-, y- and z-axes.
Any vector aligned with the x-, y- and z-axes can be defined by a scalar multiple of the unit vectors i, j and k. For example a vector 15 units long aligned with the y-axis is simply 15j. A vector 25 units long aligned with the z axis is 25k.
By employing the rules of vector addition and subtraction, we can compose a vector R by summing three Cartesian unit vectors as follows.
This is equivalent to writing R as
The magnitude of R would then be computed as
Any pair of Cartesian vectors such as R and S can be combined as follows
An example would be
Vector Multiplication
Vector multiplication provides some powerful ways of computing angles and surface orientations. While the multiplication of two scalars is a familiar operation, the multiplication of vectors is a multiplication of two 3D lines, which is not an easy operation to visualize. In vector analysis, there are generally two ways to multiply vectors: one results in a scalar value and the other one in a vector.
Scalar or Dot Product
Multiplying the magnitude of two vectors |R| and |S| is a valid operation but it ignores the orientation of the vectors, which is one of their important features. Therefore we want to include the angles between the vectors. In case of the scalar product, this is done by projecting one vector onto the other.

Figure 11 - Projecting R on S
The projection of R on S creates the basis for the scalar product, because it takes into account their relative orientation. The length of R on S is
Then we can multiply the projected length of R with the magnitude of S
or commonly written
The

Figure 12 - Dot product
The geometric representation of the dot product is useful to imagine how it works but it doesn't map well to computer hardware. The algebraic representation maps better to computer hardware and is calculated with the help of Cartesian components:
There are various dot product terms such as
Finally, terms with two vectors that are parallel to themselve lead to a value of one because the cosinus of a degree of zero is one. Additionally the Cartesian vectors are all unit vectors, which leads to
So we end up with the familiar equation
An example:
The algebraic representation results in:
The geometric representation starts out with:
Solving for the angle between the vectors by plugging in the result of the algebraic representation:
Solving for
The resulting angle will be always between
Scalar Product in Lighting Calculations
Many games utilize the Blinn-Phong lighting model (see Wikipedia; ignore the code on this page). A part of the diffuse component of this lighting model is the Lambert's Law term published in 1760. Lambert stated that the intensity of illumination on a diffuse surface is proportional to the cosine of the angle between the surface normal vector and the light source direction.
Let's assume our light source is located in our reference space for lighting at (20, 30, 40), while our normal vector is normalized and located at (0, 11, 0). The point where the intensity of illumination is measured is located at (0, 10, 0).

Figure 13 - Lighting Calculation
The light and normal vector are calculated by subtracting the position of the point where the intensity is measured -representing their tails- from their heads.
Instead of using the original light vector, the following scalar product normalizes the light vector first, before using it in the lighting equation.
To test if the light vectors magnitude is one:
Plugging the unit light vector and the unit normal vector into the algebraic representation of the scalar product.
Now solving the geometrical representation for the cosine of the angle.
In case the light and the normal vector are unit vectors, the result of the algebraic scalar product calculation equals the cosinus of the angle. The algebraic scalar product is implemented in the dot product intrinsic available for the CPU and GPU. In other words, in case the involved vectors are unit vectors, a processor can calculate the cosine of the angle faster. This is the reason why normalized vectors might be more efficient in programming computer hardware.
Following Lambert's law, the intensity of illumination on a diffuse surface is proportional to the consine of the angle between the surface normal and the light source direction. That means that the point at (0, 10, 0) receives about 0.4082 of the original light intensity at (20, 30, 40) (attenuation is not considered in this example).
Coming back to image 12, in case, the unit light vector would have a y component that is one or minus one and therefore its x and y component would be zero, it would point in the same or opposite direction as the normal and therefore the last equation would result in one or minus one. If the unit light vector would have a z or x component equaling to one and therefore the other components would be zero, those equations would result in zero.
The Vector Product
Like the scalar product, the vector or cross product depends on the modulus of two vectors and the angle between them, but the result of the vector product is essentially different: it is another vector, at right angles to both the original vectors.
and
For an understanding of the vector product R and S, it helps to imagine a plane through those two vectors as shown in figure 14.

Figure 14 - Vector Product
The angle

Figure 15 - Right-Hand rule Vector Product
The resulting vector of the cross product is perpendicular to R and S, that is
and
This makes the vector product an ideal way of computing normals. The two vectors R and S can be orthogonal but do not have to be. A property of the vector product that will be covered later is, that the magnitude of T is the area of the parallelogram defined by R and S.
Let's multiply two vectors together using the vector product.
There are various vector product terms such as
The other products between the unit vectors can be reasoned as:
Those results show, that the commutative multiplication law is not applicable to vector products. In other words
Applying those findings reduces the vector product term to
Now re-grouping the equation to bring like terms together leads to:
To achieve a visual pattern for remembering the vector product, some authors reverse the sign of the j scalar term.
Re-writing the vector product as determinants might help to memorize it as well.
A 2x2 determinant is the difference between the product of the diagonal terms. With determinants a "recipe" for a vector product consists of the following steps:
1. Write the two vectors that should be multiplied as Cartesian vectors
2. Write the cross product of those two vectors in determinant form, if this helps to memorize the process; otherwise skip to step 3.
3. Then compute by plugging in the numbers into
A simple example of a vector product calculation is to show that the assumptions that were made above, while simplifying the vector product, hold up.
To show that there is a sign reversal when the vectors are reversed
The i and k terms are both zero, but the j term is -1, which makes
Which shows
Deriving a Unit Normal Vector for a Triangle
Image 16 shows a triangle with vertices defined in anti-clockwise order. The side pointing towards the viewer is defined as the visible side in this scene. That means that the normal is expected to point roughly in the direction of where the viewer is located.

Figure 16 - Deriving a Unit Normal Vector
The vertices of the triangle are:
P1 (0, 2, 1)
P2 (0, 1, 4)
P3 (2, 0, 1)
The two vectors R and S are retrieved by subtracting the vertex at the head from the vertex at its tail.
Δx = (xh - xt)
Δy = (yh - yt)
Δz = (zh - zt)
Bringing the result into the Cartesian form
It is a common mistake to believe that if R and S are unit vectors, the cross product will also be a unit vector. The vector product equation shows that this is only true when the angle between the two vectors is 90 degrees and therefore the sinus of the angle theta is 1.
Please read in [Van Verth] about CPU implementation details.
Areas
The vector product might be used to determine the area of a parallelogram or a triangle (with the vertices at P1 - P3). Image 17 shows the two vectors helping to form a parallelogram and a triangle.

Figure 17 - Deriving the Area of a Parallelogramm / Triangle with the Vector Product
The height h is
This equals the magnitude of the cross product vector T. Thus when we calculate the vector product of R and S, the length of the normal vector equals the area of the parallelogram formed by those vectors. The triangle forms half of the parallelogram and therefore half of the area.
area of parallelogram =
area of triangle =
or
area of triangle =
To compute the surface area of a mesh constructed from triangles or parallelograms, the magnitude of its non-normalized normals can be used like this.
The sign of the magnitude of the normal shows if the vertices are clockwise or counter-clockwise oriented.
References
[Azad] Kalid Azad, "Math Better Eplained", http://betterexplained.com/articles/math-betterexplained-ebook-available/
[Eberly] David H. Eberly, "3D Game Engine Design", p. 15, 2nd Edition, Morgan Kauffman 2007
[Farin] Gerald Farin, Dianne Hansford, "The Geometry Toolbox - For Graphics and Modeling", p. 16, AK Peters 1998
[Lengyel] Eric Lengyel, Mathematics for 3D Game Programming and Computer Graphics, Second Edition, Charles River Media 2003
[Vince] John Vince, "Mathematics for Computer Graphics", Springer, 3rd Edition, 2010
[Van Verth] James M. Van Verth, Lars M. Bishop, "Essential Mathematics for Games & Interactive Applications - A Programmer's Guide", Morgan Kaufmann 2004
Subscribe to:
Posts (Atom)